1. Đường thẳng Ơ-le (Euler)
Trong một tam giác, trực tâm, trọng tâm và tâm đường tròn ngoại tiếp tam giác nằm trên một đường thẳng (gọi là đường thẳng Ơ-le).
Chứng minh:
Các điểm được đặt tên như hình vẽ: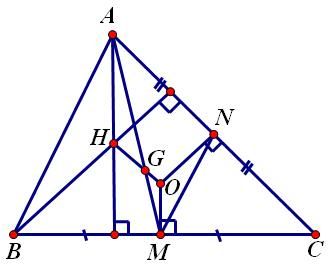

Ta có: 

Cơ mà 
Lại có: 


2. Đường tròn Ơ-le (Euler)
Trong một tam giác, chân 3 đường cao, 3 trung điểm 3 cạnh và 3 trung điểm các đoạn thẳng nối trực tâm đến đỉnh cùng nằm trên một đường tròn.
Chứng minh:
Đặt tên các điểm như hình vẽ.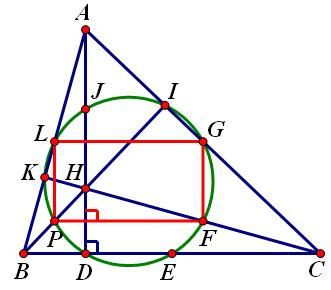

Để ý thấy  là hình chữ nhật nên nội tiếp đường tròn có tâm là trung điểm của  và . 
Tương tự:
 là hình chữ nhật nên nội tiếp đường tròn có tâm là trung điểm của và  
 là hình chữ nhật nên nội tiếp đường tròn có tâm là trung điểm của  và  
 là hình chữ nhật nên nội tiếp đường tròn có tâm là trung điểm của  và  
Từ  suy ra  điểm 
nằm trên cùng  đường tròn. (đường tròn 9 điểm - đường tròn Ơ le) 

3. Hệ thức Ơ-le (Euler)
Gọi  và  lần lượt là đường tròn ngoại tiếp và nội tiếp tam giác . Đặt . Khi đó:

Chứng minh:
Các điểm được xác định như hình vẽ.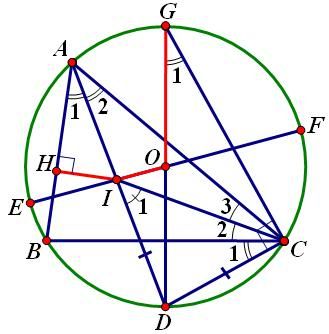

Sử dụng tính chất góc ngoài để ý thấy  cân tại .  
Ta thấy 

Từ  và  suy ra:  
Xét tam giác đồng dạng ta lại được:

Từ  và  suy ra: 

4. Định lý Lyness
Tam giác  nội tiếp đường tròn . Đường tròn  tiếp xúc trong với  tại , và tiếp xúc với  lần lượt tại . Khi đó:  đi qua tâm đường tròn nội tiếp tam giác .

Chứng minh: 
Gọi  là điểm chính giữa cung nhỏ  Gọi  là giao điểm của  và phân giác góc . Hình vẽ như sau:


mà 
Từ (1) và (2) suy ra: 
Ta có 
mà  do  cân.
Từ (3) và (4) suy ra  nội tiếp.

Suy ra HC là phân giác của 
Tương tự: HB là phân giác của 
Từ đó H là tâm đường tròn nội tiếp tam giác ABC. (đpcm) 

5. Định lý Van Oben
Tam giác  có ', ', ' đồng quy tại  thì:


Chứng minh:
Từ A kẻ đường thẳng song song với BC cắt BK và CK lần lượt tại E và D
(như hình vẽ)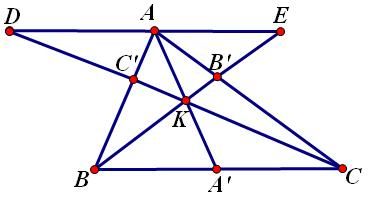

Áp dụng định lý Talet:


Các trường hợp đặc biệt:

a) Nếu AA’, BB’ CC’ là các đường trung tuyến thì:

(K khi đó gọi là trọng tâm của tam giác ABC có khoảng cách đến A bằng  đường trung tuyến)

b) Nếu AA’, BB’, CC’ là các đường phân giác trong nên: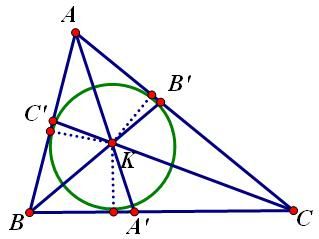


( K khi đó gọi là tâm đường tròn nội tiếp tam giác)

c) Nếu A’, B’, C’ là các tiếp điểm của đường tròn nội tiếp với các cạnh của tam giác, nên: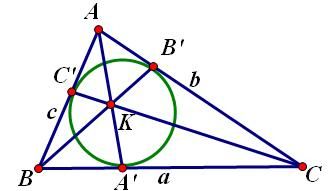



(với p là nửa chu vi)
(Khi đó K gọi là điểm Gergonne)

d) Nếu A’, B’, C’ lần lượt là tiếp điểm của các đường tròn bàng tiếp góc A, góc B, góc C với các cạnh BC, CA, AB nên: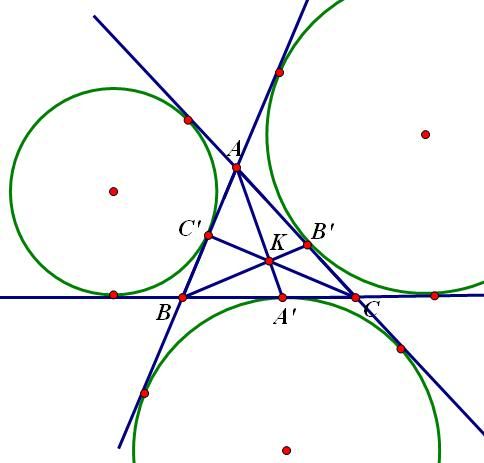



(Khi đó K gọi là điểm Nagel) 

6. Định lý hàm số cosin
Cho  nhọn nội tiếp đường tròn bán kính , có . Khi ấy thì: 

Chứng minh: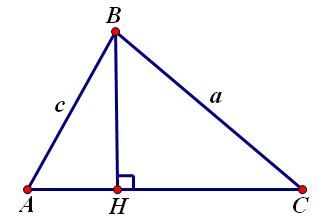

Kẻ đường cao , sử dụng định lý Pitago ta được:



7. Định lý hàm số sin.
Cho  nhọn nội tiếp  có . Khi đó thì:

(do THCS chỉ đề cập đến tỉ số lượng giác góc nhọn)

Chứng minh:
Kẻ thêm các đoạn thẳng như hình vẽ:

Ta thấy: 

tương tự:

cơ mà: 
Từ  và  suy ra đpcm. 
8. Bất đẳng thức Ptolemy
Cho tứ giác lồi  bất kỳ, ta có bất đẳng thức sau: . Đẳng thức xảy ra  là tứ giác nội tiếp.
Chứng minh: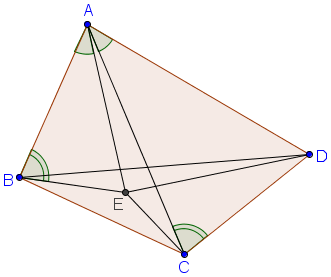

Trong tứ giác , lấy điểm  sao cho 
. Khi đó  nên  và . Suy ra 
Do đó .
Đẳng thức xảy ra  là tứ giác nội tiếp.
Từ đó suy ra định lý Ptolemy: Tứ giác lồi  là tứ giác nội tiếp 

9. Định lý Steiner-Lehmus:
Tam giác có 2 đường phân giác trong bằng nhau là tam giác cân.
Chứng minh: (R.W.Hogg-1982)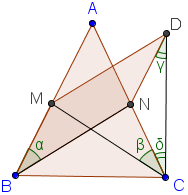

Giả sử 2 đường phân giác trong BN, CM bằng nhau
Dựng hình bình hành BMDN và kí hiệu các góc  như hình vẽ
Tam giác CMD cân tại M nên  (1)
Nếu  thì xét hai tam giác BCN và CBM có BC chung, 
mà , mâu thuẫn với (1)
Tương tự, không thể xảy ra trường hợp 
suy ra , đpcm
----------------------------
Chú dẫn lịch sử:
Năm 1840, Lehmus gửi cho Steiner bài toán trên và yêu cầu CM bằng hình học thuần túy, do đó nó mang tên Steiner-Lehmus
Trong lời giải của mình , Steiner sử dụng công thức 
sau khi biến đổi đẳng thức , ta có
, suy ra đpcm
Tuy nhiên chúng ta thấy ngay rằng cách CM của Steiner không hề mang tính hình học mà sử dụng biến đổi đại số 
Nếu các bạn muốn tìm hiểu thêm thì xem trong quyển Tuyển chọn theo chuyên đề THTT, quyển 3, trang 62-65 

10. Bất đẳng thức Erdös-Mordell
Cho tam giác  và điểm  nằm trong tam giác ( không nằm trên biên của tam giác). Gọi  là khoảng cách từ  đến các cạnh tam giác;  là khoảng cách từ  đến các đỉnh tam giác. Khi đó ta có bất đẳng thức sau 
Chứng minh:

Gọi  theo thứ tự là hình chiếu của  trên các cạnh . Lấy  đối xứng với  qua phân giác trong của góc , gọi  là hình chiếu của  trên . Gọi  là giao điểm  và ;  là hình chiếu của  trên .
Ta có . Vì  và  đối xứng với nhau qua phân giác trong góc  nên . Do đó . Tương tự, ta có 2 bất đẳng thức tương tự: . Cộng theo vế các bất đẳng thức trên và áp dụng bất đẳng thức Cauchy, ta có  (đpcm)
Đẳng thức xảy ra  đều và  là tâm của tam giác.
----------------------------
Chú dẫn lịch sử:
Nhà toán học Hungary Paul Erdös trong khi nghiên cứu tính chất của tam giác đã nêu ra bất đẳng thức trên (1935) nhưng ông không chứng minh được. Người đầu tiên chứng minh được là nhà toán học Anh Mordell. Tuy nhiên lời giải của ông (sử dụng lượng giác) chỉ mang ý nghĩa lịch sử, vì khá phức tạp và rườm rà. Đến năm 1945, mới có một lời giải thuần túy hình học có thể chấp nhận được. Tiếp theo đó đã có nhiều lời giải ngắn gọn được đưa ra. Bên trên là một lời giải chỉ sử dụng kiến thức lớp 8. 



11. Định lý Mê-nê-na-uýt (Menenaus)
Cho  có ',',' thứ tự nằm trên các đường thẳng  sao cho ',',' nằm trên phần kéo dài của 3 cạnh hoặc chỉ có 1 điểm nằm trên phần kéo dài của 3 cạnh . Điều kiện cần và đủ để 3 điểm ',',' thẳng hàng là: 

Chứng minh: (hình vẽ cho 1 điểm nằm trên phần kéo dài, trường hợp còn lại làm tương tự)
*Điều kiện cần:
Giả sử 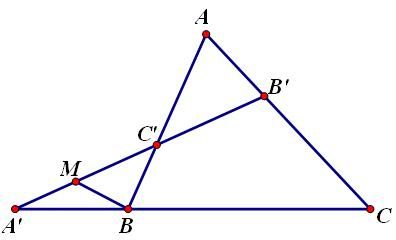 kẻ   

Dễ thấy:



 (đpcm)
*Điều kiện đủ:
Giả sử: 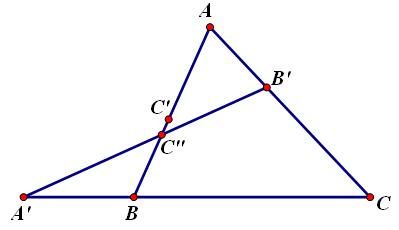 và  

Ta có:
Nhắn tin cho tác giả

Số lượt thích: 3 người (Cô nàng giấu tên, Hoàng Minh Trang, Cao Minh Tuấn Tú)